■　RSA の計算例

　さて，準備が整ったところで暗号化をしましょう。今から 1371 （cat という文字列を数値化したもの）を暗号化します。
　まず，かけ算すると 1371 より大きくなるような二つの素数を適当に選んできます。ここでは 43 と 53 にしましょう（43×53＝2279）。そして 43 と 53 という数字は秘密にし，2279 という数字は公開します（これが公開鍵の一つになります）。
　次に を計算します。この場合は

• 2279＝43×53
• 43 と 53 はともに素数
• 43 と 53 は互いに素

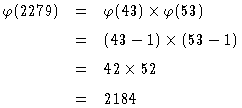
（注）UBASIC を使えば『print eul(2279)』とすることで計算可能

　次に，この 2184 と互いに素となるような数字を適当に選んできます。ここでは 1241 にしましょう（これも公開鍵の一つとなります）。

（注）UBASIC を使えば『print gcd(2184,1241)』と入力すると『 1 』となることより確認可能

　次に 2184 を法としたときの 1241 の逆元をユークリッドの互除法で求めます。

（注）UBASIC を使えば『print modinv(1241,2184)』とすることで計算可能

　すると 1649 になります（これが秘密鍵となります）。確認してみると

となることより，1649 は 1241の逆元であることが確かめられました。
　実際に割り算してみると

となります。このことは

であるということと同じです。
　少し数字が多くなってしまいましたが，整理すると

• 公開鍵は 2279 と 1241
• 秘密鍵は 1649
• 43 と 53 と 2184 は秘密

となります。この 2003 という数字が暗号文となります。

（注）UBASIC を使えば『print modpow(1371,1241,2279)』とすることで計算可能

　復号化するには秘密鍵 1649 を使って

となるので，元に戻すことが出来ます。

となります。この式は整理すると

となります。

　要領のよい人なら(2)式と(14)式を使うことによって，(6)→(12)までジャンプして考えることが可能でしょう。

■　使用上の注意点

　この例では公開鍵として 2279, 1241 の二つを使いましたが，公開鍵は一度公開してしまうと，頻繁に変更するわけにはいきません（メッセージを送る側が迷惑する）。ですから，このページの説明ではメッセージを見て公開鍵を決めているような印象を受けるかも知れませんが，実際には，まず公開鍵を決めてからそれに応じてメッセージを加工します。実際の公開鍵は200桁の数字になりますので，この範囲に収まるようにメッセージを細かく分ける等の工夫が必要となります。たとえばメッセージが長い場合は 20 文字ごとに区切って，何回かに分けて送信する等の工夫をします。

■　RSA を突破するには

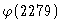　この暗号を突破するには，秘密鍵である 1649 を得る必要があるのですが 1649 は 2184 を法としたときの 1241 の逆元です。1241 は公開されているので問題はないのですが 2184 は秘密にされているので，突破するには公開されている 2279 から を計算しなくてはなりません。
　私は 2279＝43×53 であることを知っているのでオイラー関数の性質(1),(2)を使うことで容易に計算しましたが，これを知らない人は 2279 を因数分解することが必要となります。しかし，実際には200桁ほどの数字が使われますので，因数分解は限りなく不可能に近いのです。
　もちろん，「何となく思いついた数字で割り算したら割り切れた（つまり偶然因数分解出来てしまった）。ラッキー！」なんてことがないとは言い切れませんが，その可能性もほとんどないでしょう。
　以上のような理由から RSA の安全性が（現在のところ）確認されています。

前へ　次へ

メニューへ戻る