モジュラス数学とは，割り算をしたときの余りだけに着目する数学です。 例として 13 を基準として考えてみましょう。13 を基準とすることを13を法とするといいます。57 を 13 で割り算すると
となるので，13 を法としたとき 57 と 5 は同じ数字だと考えます。このことを
と書きます。他の例をあげると
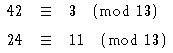
となりますね。
かけ算をするときは 3 に
となることより，5 の逆元は 8 となります。ユークリッドの互除法という計算を行うことで逆元は容易に計算が可能です。
繰り返し二乗法は
コンピュータ内では何回かけ算をしたかが重要な問題となりますので
全部で 4 回のかけ算で済ますことが出来ました。同様にして，
となりますね。
オイラー関数
例として
であることから
例として 13 は素数だから，
ですから
例として
同様に
例として 13 は素数であるので，
となる。
実際は
という具合に繰り返し二乗法と13を法とした計算を組み合わせて大きな数字を扱わないようにすることで，効率よく計算出来ます。
例として m = 15 とすると
となることより
そこで
であることより
となり，定理が正しいことが確かめられた。
実際には 15を法として考えればよいので，フェルマーの定理のところで説明したようにこのように大きな数字は扱わずに済む。
例として次のように書いた方が分かり易いかな？。
となるので
のような計算をした方が簡単だ！。
例として次のように書いた方が分かり易いかな？。
となるので
のような計算をした方が簡単だ！。
■ 逆元
をかけると 1 となります。このようにある数字に対してかけ算すると 1 になるような数字のことを逆元といいます（かけ算の場合は逆数という呼び方が一般的です）。13 を法としたとき，5 の逆元を求めてみましょう。
■ 繰り返し二乗法
のような計算を効率的に計算する計算法です。そのままかけ算すると 9 回のかけ算をしなくてはなりませんが，次のようにするとかけ算の回数を減らすことが出来ます。
の計算でも 9 回のかけ算で済ますことができますので，繰り返し二乗法を使うことでアッという間に計算できます。■ 最大公約数
の最大公約数を 
と書くことにします。または（書くのが面倒くさいので）もっと手抜きをして単に 
と書くことにします（gcd は greatest common divisor の意味，中学校や高校の教科書では gcm (greatest common measure) と書かれている。）。特に 
となるとき は互いに素であるといいます。例を挙げると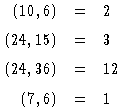
■ オイラー関数
とは 
である整数 
のうち 
となる整数の個数のことである。
とは 
である整数（つまり 
）のうち 
となる整数（つまり互いに素である整数）の個数のことなので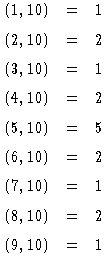
の 4個ということになり 
となります。オイラー関数については次の性質が成り立つ。■ オイラー関数の性質(1)
が素数ならば，
となる。
となる。なぜなら 
とは 
である整数（つまり 
）のうち 
となる整数の個数のことであるが，13 は素数なので のいずれの数とも互いに素となるのは当たり前です。もし，互いに素でない数が見つかれば約数が見つかったことになり，13 が素数であるという仮定に反します。 が素数のときはオイラー関数の計算は極めて簡単です。（合成数のときは少し工夫が必要となります）■ オイラー関数の性質(2)
ならば，
となる。
なので，
と計算することが可能である。（オイラー関数の性質(1)を使った。）
なので 
までは計算できますが，
は 12 が素数でないので簡単には計算できません。 の計算については参考文献をご覧下さい。■ フェルマーの定理
を素数とする。このとき 
であるどのような に対しても 
が成り立つ。
となる全ての に対して 
となる。具体的には
の計算は
■ オイラーの定理
を正の整数とする（素数である必要はない）。このとき 
であれば 
が成り立つ。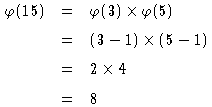
であれば 
が成り立つということであると書き直せる。
のうち，15 と互いに素であるものを求めると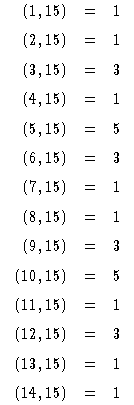
となる。実際に計算してみると
■ 指数法則(1)
が成り立つ。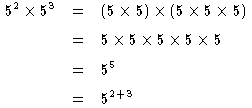
■ 指数法則(2)
が成り立つ。
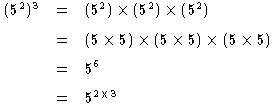
前へ 次へ 